From ASCII to ASIC: Porting donut.c to a tiny slice of silicon

Jan 10, 2025

For many years after coming up with donut.c, I wondered in the back of my mind if it could be simplified somehow, like maybe there was a way to raytrace a donut with a small chunk of code. In October 2023, I tweeted a dumb random epiphany where I figured out another way to do it which requires no memory, no sines or cosines, no square roots, no divisions, and technically, not even any multiplications. The whole thing can be rendered with just shifts and adds, and there's an updated C version here.

It took almost another year to put this idea into action with an actual hardware implementation. In early September 2024, I submitted a 4-tile design to Tiny Tapeout 8, taking up 0.8% of a 130nm process chip shared with many other designs. This chip is currently (as of January 2025) being manufactured by SkyWater Technologies, and if my design works, it will render this to a VGA monitor:

This design is not rendering polygons! Instead, it's making an iterative approximation of a ray-traced donut, and it is racing the VGA beam — every 39 nanoseconds, the monitor is going to show the next pixel, ready or not, practical considerations limit us to a ~50MHz clock, and we have no memory buffer whatsoever — so it doesn't have enough time to do a good job; the polygonal appearance is a complete accident!

And no, I already know what you're going to ask: the actual silicon is not in the shape of a donut. Maybe next time. It takes about 7000 standard cells (i.e., flip flops or logic gates), and you can actually see a 3D view of the die here thanks to the amazing tools the Tiny Tapeout team has put together.

With more die area, and/or a faster clock (which would need something more modern than the 130nm SkyWater process), this could be pipelined so that every pixel was perfectly rendered, but the point was to make it as small as I could.

Source

The TinyTapeout Verilog project is on github here with a Verilator testbench which produced the above video and an OrangeCrab FPGA version I used to develop.

Because I developed it on an OrangeCrab, I ended up using its native 48MHz clock for all timing; typically VGA would have a 25.175MHz clock, so I opted to use a slighly strange VGA mode of 1220x480 in order to have the timing work out. This looks great on an analog CRT, but LCD monitors can end up with weird aliasing artifacts. Lesson learned.

I have this and two other designs (which deserve their own write-ups!) on Tiny Tapeout 8 and they were my first real Verilog projects; the code is frankly atrocious in order to get everything to fit under tight constraints.

Rendering donuts with just shifts and adds

The trick is to represent the torus as a signed distance function and "raymarch" it, which is a shockingly powerful technique popularized by Inigo Quilez, who does incredible work. His site is a treasure trove in general, but see this excerpt from his distance functions page:

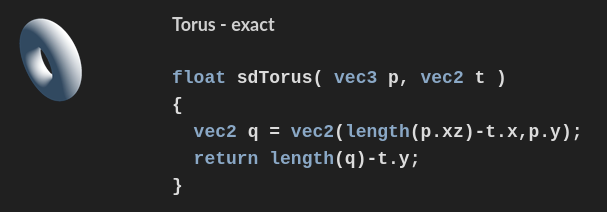
The signed distance to a torus can be computed by two 2-dimensional length operations in sequence. Guess how you can compute the length of a 2D vector? With CORDIC, a variation on the same trick I used last time!

The implication of this is that you can find the intersection of a ray and a donut by ray marching: starting at the 3D location of the screen, calculate the above function to find the distance; then, move that distance along the ray between the origin and the pixel you are rendering, and repeat the whole process until the distance converges near 0.

That gives you the point, but what color do we actually render? We need the surface normal to compute lighting, which requires rotating the light direction vector along the two axes of the torus with whatever angle we happened to hit it at. This seemed way too complicated at first.

The random epiphany I had was this: the amount we need to rotate the lighting vector to find the surface normal is exactly the same as the rotations we undid to find the distance to the torus in the first place! And furthermore, we can do this rotation almost for free as a side effect of computing those lengths.

Let me try to explain.

Vectoring mode CORDIC

There's a trick where you can compute \sqrt{x^2 + y^2} using only shifts and adds, a profoundly clever application of CORDIC: you iteratively rotate the \overrightarrow{(x,y)} vector toward the x axis, one "bit" at a time (first by \arctan 1= 45°, by \arctan \frac{1}{2} = 26.5°, \arctan \frac{1}{4} = 14.04°, etc). This not only allows you to recover the length but also the angle, in effect transforming between Cartesian and polar coordinates.

The above widget is running this code for eight iterations and drawing all the intermediate steps in various colors, with the bold green line being the final iteration:

function cordicLength(x, y, n) {
    // x must be in right half-plane; since we only really care about distance, we
    // discard the fact that we did this, but we could set a flag to recover the
    // correct angle here.
    if (x < 0) {
        x = -x;
    }
    for (var i=0; i < n; i++) {
        var t = x;
        if (y < 0) {
            x -= y>>i;
            y += t>>i;
        } else {
            x += y>>i;
            y -= t>>i;
        }
    }
    return x;
}

The way this works is that the shifts and adds here perform a rotation and scale; effectively doing this matrix multiplication:

If the point is above the x-axis, we rotate it clockwise, otherwise rotate it counterclockwise, making smaller and smaller adjustments. The angles we're rotating by are \theta_i = \arctan 2^{-i}.

The obvious problem, and you can see it in the iterations above, is that each one of these operations isn't just rotating but also making the vector longer. However, it always makes it longer by the same amount, because we're always doing the same rotations (just changing the sign of them). This works out to a scale factor of about 0.607. So if we keep track of how much we've pre-scaled the lengths by doing this operation, we can correct for it later.

Vectoring an extra vector

By making a small tweak, we can rotate (and scale, by the same .607 factor) a second vector by the angle of the original vector in the process of finding the original vector's length.

Now if blue vector \overrightarrow{(x_2, y_2)} is our "extra" vector, the black vector \overrightarrow{(x,y)} is the one we want to find the length of, and the green line finds the relative angle between the two vectors, independent of the length of (x,y).

function rotateCordic(x, y, x2, y2, n) {
    xsign = 1;
    // if we're in the left half-plane, then negating the input x, y and the
    // output x2, y2 will give the correct result
    if (x < 0) {
        x = -x;
        y = -y;
        xsign = -1;
    }
    for (var i=0; i < n; i++) {
        var t = x;
        var t2 = x2;
        if (y < 0) {
            x -= y>>i;
            y += t>>i;
            x2 -= y2>>i;
            y2 += t2>>i;
        } else {
            x += y>>i;
            y -= t>>i;
            x2 += y2>>i;
            y2 -= t2>>i;
        }
    }
    // x is now the length of x,y and [x2*xsign, y2*xsign] is the rotated vector
    return [x, x2*xsign, y2*xsign];
}

tweaked CORDIC function to rotate an auxiliary vector

This is exactly what we need to compute lighting: if we feed in the lighting direction unit vector and the surface normal, the x coordinate of the green line is the cosine of the angle between them; we've managed to do a vector dot product without any multiplications as a side effect while computing a distance.

How do we know what the surface normal is? Well, it turns out that when the ray-marching converges, the points we're taking lengths of are relative to the center ring of the torus, so they point in the direction of the surface normal by definition.

Here's a little animation illustrating the process of finding the closest point on a torus: first, you find the point in the center ring of the torus closest to your point, which is equivalent to projecting your point onto the torus's x-z plane and scaling the distance to r_1. This new point is the center of a ring of radius r_2 in the plane defined by that point, the original point, and the center of the torus. Then, do another projection of the original point in that plane out to a distance of r_2.

float distance_to_torus(float x, float y, float z, float r1, float r2) {
  // First, we find the distance from point p to a circle of radius r1 on the x-z plane
  float dist_to_r1_circle = length(x, z) - r1;
  // Then, find the distance in the cross section of the torus from the center ring to point p
  return length(dist_to_r1_circle, y) - r2;
}

That last projection line drawn to calculate the final distance between the torus and the point is exactly the surface normal.

It is this two-2D length property of toruses that makes this whole technique possible; I haven't been able to come up with a similar way to render a sphere for instance, which you would think is easier!

Ray-marched donut.c

With this technique in hand, I came up with yet another donut.c (source here), shifts and adds only. It's not very compact as it takes a lot more C code, but it takes a lot fewer logic gates. Soon after I tweeted it out, Bruno Levy replied with an interesting discovery: if you restrict the number of CORDIC iterations, the donut renders with facets instead of smoothly!

In the final ASIC version, I used 3 r_1 iterations and 2 for r_2, because that was as much combinational logic as I could unroll in a single cycle at 48MHz and still meet setup/hold time requirements. That's why the rendering looks the way it does.

Compound rotation without multiplication

The rotation of the object as a whole is implemented by tracking eight variables: sin/cos of angle A, sin/cos of angle B, and four specific products thereof. In the C code, this is done towards the bottom with a rotation macro R():

    R(5, cA, sA);
    R(5, cAsB, sAsB);
    R(5, cAcB, sAcB);
    R(6, cB, sB);
    R(6, cAcB, cAsB);
    R(6, sAcB, sAsB);

These are all the products necessary to reconstruct the camera origin and ray directions without explicitly constructing a matrix or direction vector.

Unfortunately, this can drift over time resulting in a very skewed looking render, so there's a hack to reinitialize all of these to their zero-rotation values when a full cycle through A and B complete.

TinyTapeout considerations

TinyTapeout recommended using up to 50MHz for the clock, so I went with 48MHz (the default clock of my FPGA dev board), giving me about 1220 clocks per visible horizontal scanline. By cutting back on precision, I was able to stuff all of the CORDIC iterations into one cycle, but ray-marching needs to iterate until convergence, and any fewer than 8 iterations looked pretty bad, so I chose to iterate 8 times, reading the output of the hardware ray marching unit and loading new ray directions in every 8 clocks. But in order to keep it from looking too blocky, the horizontal offset is dithered both in space and time, which is what gives the glitchy/noisy appearance in the video.

Video output is provided through the Tiny VGA Pmod which has only two bits per RGB channel. To deal with this I chose to do ordered dithering, using 6 bits of internal color depth, and this turns out to be very easy to do in Verilog. This generates a dithering matrix which alternates every frame, yielding temporal dithering as well.

// Bayer dithering
// this is a 8x4 Bayer matrix which gets flipped every frame
wire [2:0] bayer_i = h_count[2:0] ^ {3{frame[0]}};
wire [1:0] bayer_j = v_count[1:0];
wire [2:0] bayer_x = {bayer_i[2], bayer_i[1]^bayer_j[1], bayer_i[0]^bayer_j[0]};
wire [4:0] bayer = {bayer_x[0], bayer_i[0], bayer_x[1], bayer_i[1], bayer_x[2]};

This generates a matrix that looks like this, and mirrors horizontally on alternating frames:

This is applied to the 6-bit color like so:

// output dithered 2 bit color from 6 bit color and 5 bit Bayer matrix
function [1:0] dither2;
    input [5:0] color6;
    input [4:0] bayer5;
    begin
        dither2 = ({1'b0, color6} + {2'b0, bayer5} + color6[0] + color6[5] + color6[5:1]) >> 5;
    end
endfunction

wire [1:0] rdither = dither2(r, bayer);
wire [1:0] gdither = dither2(g, bayer);
wire [1:0] bdither = dither2(b, bayer);

Avoiding the last multiplication

Another challenge was stepping a 3D unit vector along a specified distance in order to do the ray-marching. Ideally this would have 3 parallel 14-bit multiplies, but I was running out of gate area, and didn't want to unroll it over multiple clock cycles. Seeing as the incoming distance was approximate anyway, I opted for an approximate multiplier which finds the leading 1 bit and returns a shifted copy of the unit vector as a step direction.

Wrapping up

From obfuscated C code printing ASCII art, to bitwise operations rendering 3D graphics, and finally to a tiny slice of silicon racing an electron beam, this project shows how the same basic idea can be reimagined and refined. What started as a fun programming puzzle led to discovering an elegant way to render 3D graphics with minimal computational resources. While the original donut.c was an exercise in creative constraint — fitting a 3D renderer into as little code as possible — this hardware implementation pushed different limits: how few gates, how few operations per pixel could still produce a recognizable rotating donut?

The polygonal appearance that emerged from limiting CORDIC iterations was a happy accident, a reminder that sometimes the most interesting results come from working within tight constraints.

Tiny Tapeout 8 is estimated to deliver chips in May 2025; it is currently January and I cannot wait. This chip also hosts the inaugural Tiny Tapeout Demoscene Competition; it may be the coolest ASIC ever made. I also have a democompo entry which I will write about once judging is done.